Å! 42+ Vanlige fakta om Sin(A+B)! Ignore a/sin a (not useful to us):

Sin(A+B) | Alex thank you exactly what i needed Note that you can get (5) from (4) by replacing b with −b, and using the fact that cos(−b) = cos b (cos is even) and sin by putting a = b = θ. Cos a + cos b = 2 cos. Now we use our algebra skills to rearrange and solve in this case it is best to turn the fractions upside down ( sin a/a instead of a/sin a , etc) We will learn how to find the expansion of sin (a + b + c).

Ignore a/sin a (not useful to us): Cos a + cos b = 2 cos. Now we use our algebra skills to rearrange and solve in this case it is best to turn the fractions upside down ( sin a/a instead of a/sin a , etc) We will learn how to find the expansion of sin (a + b + c). Note that you can get (5) from (4) by replacing b with −b, and using the fact that cos(−b) = cos b (cos is even) and sin by putting a = b = θ.

Ex: Find sin(a+b) and cos(a-b) given sin(a) and cos(b ... from i.ytimg.com

Alex thank you exactly what i needed Cos a + cos b = 2 cos. Ignore a/sin a (not useful to us): Note that you can get (5) from (4) by replacing b with −b, and using the fact that cos(−b) = cos b (cos is even) and sin by putting a = b = θ. By using the formula of sin (α + β) and cos (α + β) we can easily expand sin (a + b + c). We will learn how to find the expansion of sin (a + b + c). Now we use our algebra skills to rearrange and solve in this case it is best to turn the fractions upside down ( sin a/a instead of a/sin a , etc)

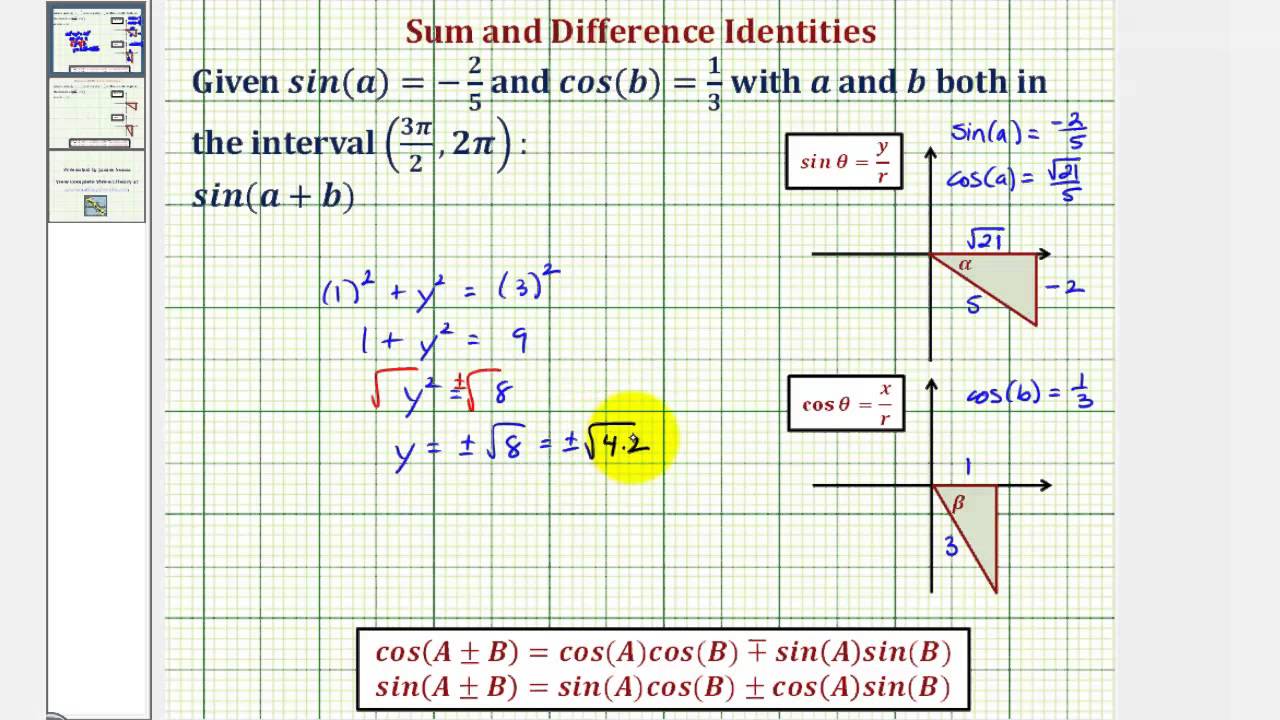
Note that you can get (5) from (4) by replacing b with −b, and using the fact that cos(−b) = cos b (cos is even) and sin by putting a = b = θ. By using the formula of sin (α + β) and cos (α + β) we can easily expand sin (a + b + c). Alex thank you exactly what i needed We will learn how to find the expansion of sin (a + b + c). Cos a + cos b = 2 cos. Ignore a/sin a (not useful to us): Now we use our algebra skills to rearrange and solve in this case it is best to turn the fractions upside down ( sin a/a instead of a/sin a , etc)

Cos a + cos b = 2 cos. By using the formula of sin (α + β) and cos (α + β) we can easily expand sin (a + b + c). Ignore a/sin a (not useful to us): Note that you can get (5) from (4) by replacing b with −b, and using the fact that cos(−b) = cos b (cos is even) and sin by putting a = b = θ. Now we use our algebra skills to rearrange and solve in this case it is best to turn the fractions upside down ( sin a/a instead of a/sin a , etc)

Ex: Find sin(a+b) and cos(a-b) given sin(a) and cos(b ... from i.ytimg.com

Note that you can get (5) from (4) by replacing b with −b, and using the fact that cos(−b) = cos b (cos is even) and sin by putting a = b = θ. Alex thank you exactly what i needed By using the formula of sin (α + β) and cos (α + β) we can easily expand sin (a + b + c). Cos a + cos b = 2 cos. Now we use our algebra skills to rearrange and solve in this case it is best to turn the fractions upside down ( sin a/a instead of a/sin a , etc) We will learn how to find the expansion of sin (a + b + c). Ignore a/sin a (not useful to us):

Ignore a/sin a (not useful to us): Alex thank you exactly what i needed Cos a + cos b = 2 cos. Now we use our algebra skills to rearrange and solve in this case it is best to turn the fractions upside down ( sin a/a instead of a/sin a , etc) We will learn how to find the expansion of sin (a + b + c). Note that you can get (5) from (4) by replacing b with −b, and using the fact that cos(−b) = cos b (cos is even) and sin by putting a = b = θ. By using the formula of sin (α + β) and cos (α + β) we can easily expand sin (a + b + c).

We will learn how to find the expansion of sin (a + b + c). Cos a + cos b = 2 cos. Now we use our algebra skills to rearrange and solve in this case it is best to turn the fractions upside down ( sin a/a instead of a/sin a , etc) By using the formula of sin (α + β) and cos (α + β) we can easily expand sin (a + b + c). Ignore a/sin a (not useful to us):

Example 8 - If sin (A - B) = 1/2, cos (A + B) = 1/2, find A from d77da31580fbc8944c00-52b01ccbcfe56047120eec75d9cb2cbd.ssl.cf6.rackcdn.com

Ignore a/sin a (not useful to us): By using the formula of sin (α + β) and cos (α + β) we can easily expand sin (a + b + c). Cos a + cos b = 2 cos. Now we use our algebra skills to rearrange and solve in this case it is best to turn the fractions upside down ( sin a/a instead of a/sin a , etc) We will learn how to find the expansion of sin (a + b + c). Alex thank you exactly what i needed Note that you can get (5) from (4) by replacing b with −b, and using the fact that cos(−b) = cos b (cos is even) and sin by putting a = b = θ.

We will learn how to find the expansion of sin (a + b + c). By using the formula of sin (α + β) and cos (α + β) we can easily expand sin (a + b + c). Now we use our algebra skills to rearrange and solve in this case it is best to turn the fractions upside down ( sin a/a instead of a/sin a , etc) Cos a + cos b = 2 cos. Alex thank you exactly what i needed Note that you can get (5) from (4) by replacing b with −b, and using the fact that cos(−b) = cos b (cos is even) and sin by putting a = b = θ. Ignore a/sin a (not useful to us):

Sin(A+B): By using the formula of sin (α + β) and cos (α + β) we can easily expand sin (a + b + c).

Source: i.ytimg.com

Ignore a/sin a (not useful to us): Now we use our algebra skills to rearrange and solve in this case it is best to turn the fractions upside down ( sin a/a instead of a/sin a , etc) We will learn how to find the expansion of sin (a + b + c). Note that you can get (5) from (4) by replacing b with −b, and using the fact that cos(−b) = cos b (cos is even) and sin by putting a = b = θ. Cos a + cos b = 2 cos.

Source: i.ytimg.com

Cos a + cos b = 2 cos. Alex thank you exactly what i needed Now we use our algebra skills to rearrange and solve in this case it is best to turn the fractions upside down ( sin a/a instead of a/sin a , etc)

Source: i.ytimg.com

By using the formula of sin (α + β) and cos (α + β) we can easily expand sin (a + b + c). We will learn how to find the expansion of sin (a + b + c). Ignore a/sin a (not useful to us):

Source: d77da31580fbc8944c00-52b01ccbcfe56047120eec75d9cb2cbd.ssl.cf6.rackcdn.com

Cos a + cos b = 2 cos. Note that you can get (5) from (4) by replacing b with −b, and using the fact that cos(−b) = cos b (cos is even) and sin by putting a = b = θ. Alex thank you exactly what i needed

Referanse: Sin(A+B)